定点数这玩意儿并不是什么新东西,早年 CPU 浮点性能不够,定点数技巧大量活跃于各类图形图像处理的热点路径中。今天 CPU 浮点上来了,但很多情况下整数仍然快于浮点,因此比如:libcario (gnome/quartz 后端)及 pixman 之类的很多库里你仍然找得到定点数的身影。那么今天我们就来看看使用定点数到底能快多少。
简单用一下的话,下面这几行宏就够了:
#define cfixed_from_int(i) (((cfixed)(i)) << 16)
#define cfixed_from_float(x) ((cfixed)((x) * 65536.0f))
#define cfixed_from_double(d) ((cfixed)((d) * 65536.0))
#define cfixed_to_int(f) ((f) >> 16)
#define cfixed_to_float(x) ((float)((x) / 65536.0f))
#define cfixed_to_double(f) ((double)((f) / 65536.0))
#define cfixed_const_1 (cfixed_from_int(1))
#define cfixed_const_half (cfixed_const_1 >> 1)
#define cfixed_const_e ((cfixed)(1))
#define cfixed_const_1_m_e (cfixed_const_1 - cfixed_const_e)
#define cfixed_frac(f) ((f) & cfixed_const_1_m_e)
#define cfixed_floor(f) ((f) & (~cfixed_const_1_m_e))
#define cfixed_ceil(f) (cfixed_floor((f) + 0xffff))
#define cfixed_mul(x, y) ((cfixed)((((int64_t)(x)) * (y)) >> 16))
#define cfixed_div(x, y) ((cfixed)((((int64_t)(x)) << 16) / (y)))
#define cfixed_const_max ((int64_t)0x7fffffff)
#define cfixed_const_min (-((((int64_t)1) << 31)))
typedef int32_t cfixed;
类型狂可以写成 inline 函数,封装狂可以封装成一系列 operator xx,如果需要更高的精度,可以将上面用 int32_t 表示的 16.16 定点数改为用 int64_t 表示的 32.32 定点数。
那么我们找个浮点数的例子优化一下吧,比如 libyuv 中的 ARGBAffineRow_C 函数:
void ARGBAffineRow_C(const uint8_t* src_argb,
int src_argb_stride,
uint8_t* dst_argb,
const float* uv_dudv,
int width) {
int i;
// Render a row of pixels from source into a buffer.
float uv[2];
uv[0] = uv_dudv[0];
uv[1] = uv_dudv[1];
for (i = 0; i < width; ++i) {
int x = (int)(uv[0]);
int y = (int)(uv[1]);
*(uint32_t*)(dst_argb) = *(const uint32_t*)(src_argb + y * src_argb_stride + x * 4);
dst_argb += 4;
uv[0] += uv_dudv[2];
uv[1] += uv_dudv[3];
}
}
这个函数是干什么用的呢?给图像做 仿射变换(affine transformation) 用的,比如 2D 图像库或者 ActionScript 中可以给 Bitmap 设置一个 3×3 的矩阵,然后让 Bitmap 按照该矩阵进行变换绘制:

基本上二维图像所有:缩放,旋转,扭曲都是通过仿射变换完成,这个函数就是从图像的起点(u, v)开始按照步长(du, dv)进行采样,放入临时缓存中,方便下一步一次性整行写入 frame buffer。
这个采样函数有几个特点:
- 运算简单:没有复杂的运算,计算无越界,不需要求什么 log/exp 之类的复杂函数。
- 范围可控:大部分图像长宽尺寸都在 32768 范围内,用 16.16 的定点数即可。
- 转换频繁:每个点的坐标都需要从浮点转换成整数,这个操作很费事。
适合用定点数简单重写一下:(点击 Read more 展开)
void ARGBAffineRow_Fixed(const uint8_t* src_argb,
int src_argb_stride,
uint8_t* dst_argb,
const float* uv_dudv,
int width) {
int32_t u = (int32_t)(uv_dudv[0] * 65536); // 浮点数转定点数
int32_t v = (int32_t)(uv_dudv[1] * 65536);
int32_t du = (int32_t)(uv_dudv[2] * 65536);
int32_t dv = (int32_t)(uv_dudv[3] * 65536);
for (; width > 0; width--) {
int x = (int)(u >> 16); // 定点数坐标转整数坐标
int y = (int)(v >> 16);
*(uint32_t*)(dst_argb) = *(const uint32_t*)(src_argb + y * src_argb_stride + x * 4);
dst_argb += 4;
u += du; // 定点数加法
v += dv;
}
}
局部用一下定点数都不需要定义前面那一堆宏,按相关原理直接写就是了。
我们用 llvm-mca 分析一下,浮点数版本 gcc 9.0 的循环主体部分用 -O3 的代码生成:
Iterations: 100
Instructions: 1300
Total Cycles: 458
Total uOps: 1500
Dispatch Width: 6
uOps Per Cycle: 3.28
IPC: 2.84
Block RThroughput: 3.0
Instruction Info:
[1]: #uOps
[2]: Latency
[3]: RThroughput
[4]: MayLoad
[5]: MayStore
[6]: HasSideEffects (U)
[1] [2] [3] [4] [5] [6] Instructions:
2 6 1.00 cvttss2si eax, xmm1
1 1 0.25 add rsi, 4
1 4 0.50 addss xmm1, xmm2
2 6 1.00 cvttss2si edx, xmm0
1 4 0.50 addss xmm0, xmm3
1 3 1.00 imul eax, r9d
1 1 0.50 shl edx, 2
1 1 0.25 cdqe
1 1 0.25 add rax, rdi
1 5 0.50 * mov eax, dword ptr [rax + rdx]
1 1 1.00 * mov dword ptr [rsi - 4], eax
1 1 0.25 cmp rsi, rcx
1 1 0.50 jne .L3
链接:https://godbolt.org/z/HGPCHA
可以看到,虽然编译器自动生成了 sse 代码,但性能消耗的大户,cvttss2si(浮点数转整数指令),虽然只有一条命令,但会生成两个微指令(uOP),延迟 6 个周期,rthroughput 很高 1.0 代表每周期只能同时运行一条该指令,其次是加法指令 addss, 延迟是 4 个周期,吞吐量 0.5 代表每周期可以并行执行 2 条,该代码块模拟运行 100 次,总消耗 458 个周期。
再看定点数版本:
Iterations: 100
Instructions: 1500
Total Cycles: 337
Total uOps: 1500
Dispatch Width: 6
uOps Per Cycle: 4.45
IPC: 4.45
Block RThroughput: 2.5
Instruction Info:
[1]: #uOps
[2]: Latency
[3]: RThroughput
[4]: MayLoad
[5]: MayStore
[6]: HasSideEffects (U)
[1] [2] [3] [4] [5] [6] Instructions:
1 1 0.25 mov eax, edi
1 1 0.25 mov edx, ecx
1 1 0.25 add rsi, 4
1 1 0.25 add ecx, r11d
1 1 0.50 sar eax, 16
1 1 0.50 sar edx, 16
1 1 0.25 add edi, ebx
1 3 1.00 imul eax, r10d
1 1 0.50 shl edx, 2
1 1 0.25 cdqe
1 1 0.25 add rax, r9
1 5 0.50 * mov eax, dword ptr [rax + rdx]
1 1 1.00 * mov dword ptr [rsi - 4], eax
1 1 0.25 cmp rsi, r8
1 1 0.50 jne .L8
链接:https://godbolt.org/z/Adj9gQ
指令虽然多了两条,但是整数指令 latency 比浮点要低,并且吞吐量(并行性)比浮点更好,大部分指令都是 0.25,代表每周期可以并行执行四条,模拟运行 100 次,总消耗 337 个周期。
这里你可能要问,整数版本,第二列 latency 加起来有 21 个周期啊,为什么平均运行一次才 3.37 个周期呢?这就是多级流水线中很多指令可以并行运行,只要没有运算结果依赖,以及没有执行单元的资源冲突,很多运算都是可以并行的,所以优化里,运算解依赖很有用。
我们给 llmv-mca 加一个 -timeline 参数,能得到流水线分析报表,这里截取两次循环:
[0,0] DeER . . . . . . . . . mov eax, edi
[0,1] DeER . . . . . . . . . mov edx, ecx
[0,2] DeER . . . . . . . . . add rsi, 4
[0,3] DeER . . . . . . . . . add ecx, r11d
[0,4] D=eER. . . . . . . . . sar eax, 16
[0,5] D=eER. . . . . . . . . sar edx, 16
[0,6] .DeER. . . . . . . . . add edi, ebx
[0,7] .D=eeeER . . . . . . . . imul eax, r10d
[0,8] .D=eE--R . . . . . . . . shl edx, 2
[0,9] .D====eER . . . . . . . . cdqe
[0,10] .D=====eER. . . . . . . . add rax, r9
[0,11] .D======eeeeeER. . . . . . . mov eax, dword ptr [rax + rdx]
[0,12] . D==========eER . . . . . . mov dword ptr [rsi - 4], eax
[0,13] . DeE----------R . . . . . . cmp rsi, r8
[0,14] . D=eE---------R . . . . . . jne .L8
[1,0] . DeE----------R . . . . . . mov eax, edi
[1,1] . D=eE---------R . . . . . . mov edx, ecx
[1,2] . D=eE---------R . . . . . . add rsi, 4
[1,3] . DeE---------R . . . . . . add ecx, r11d
[1,4] . D=eE--------R . . . . . . sar eax, 16
[1,5] . D=eE--------R . . . . . . sar edx, 16
[1,6] . D=eE--------R . . . . . . add edi, ebx
[1,7] . D==eeeE-----R . . . . . . imul eax, r10d
[1,8] . D==eE-------R . . . . . . shl edx, 2
[1,9] . D====eE----R . . . . . . cdqe
[1,10] . D=====eE---R . . . . . . add rax, r9
[1,11] . D======eeeeeER . . . . . . mov eax, dword ptr [rax + rdx]
[1,12] . D===========eER . . . . . . mov dword ptr [rsi - 4], eax
[1,13] . DeE-----------R . . . . . . cmp rsi, r8
[1,14] . D==eE---------R . . . . . . jne .L8
每条指令有下面几个生存周期:
D : Instruction dispatched.
e : Instruction executing.
E : Instruction executed.
R : Instruction retired.
= : Instruction already dispatched, waiting to be executed.
- : Instruction executed, waiting to be retired.
`````
可以看到无依赖的头四条指令:
```bash
[0,0] DeER . . . . . . . . . mov eax, edi
[0,1] DeER . . . . . . . . . mov edx, ecx
[0,2] DeER . . . . . . . . . add rsi, 4
[0,3] DeER . . . . . . . . . add ecx, r11d
从分发(D),执行(e),完成执行(E)到退休(R),基本都是同时进行的。后面两条指令虽然也是和前面四条一起分发(D),但由于依赖头两条指令的运算结果,所以产生了一个周期的等待(=):
[0,4] D=eER. . . . . . . . . sar eax, 16
[0,5] D=eER. . . . . . . . . sar edx, 16
等到头两个指令执行成功(e 结束),他们才能开始执行,第二次迭代 [1,0] 类似,多次迭代虽然用到了同样的寄存器,但是在 CPU 里 eax 只是个名字,CPU 对无关运算的寄存器进行重命名后,其实背后对应到了不同的寄存器地址,第二次迭代又有很多地方可以和第一次迭代并行执行,所以我们会发现两次迭代的最后一条指令 [0,14] 和 [1,14] 处理的退休时间 R 都差不多,两次循环几乎是并行执行的,如此多次循环平摊下来每次只要 3.37 个周期。
可以发现比浮点数版本的 4.58 个周期快了 35% 左右,注意一点,实际 I/O 操作会占用更多时间,所以在 mca 的分析里都标注了 MayLoad / MayStore,所以算上 I/O,两边的周期数都会略有增加,但是优势还在那里。
使用 mca 进行分析的时候,你把编译结果贴过去时,只能贴循环的主体部分,因为本身就要进行多次运行的流水线模拟,所以你贴了循环外的初始化部分就会干扰分析结果。
可能有人会说,妈呀,静态性能分析还要计算流水线么?其实大部分时候不需要,没有 llvm-mca 的时候我们做静态性能分析一般就是查指令手册:
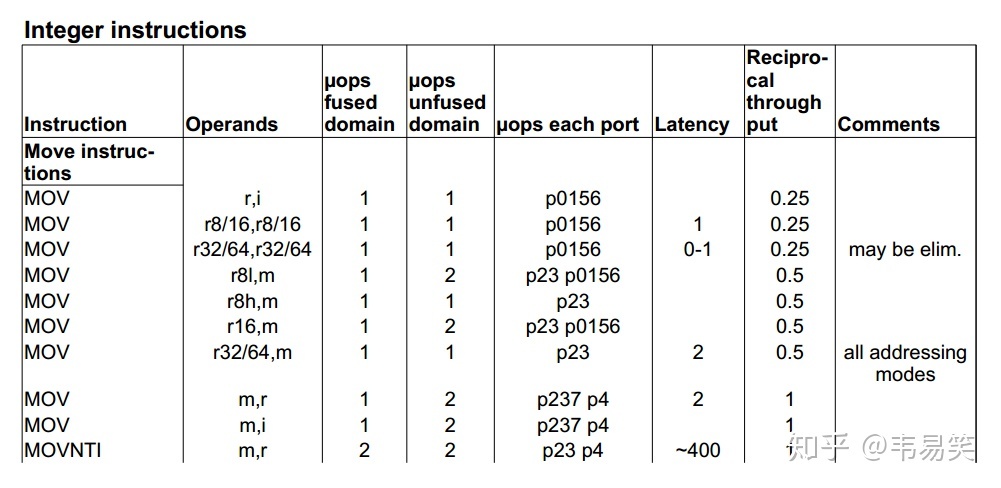
大部分时候,看一下 uops 数量(越少越好),看一下周期 latency(越少越好),以及 throughput (决定并行效率,越低越好),心中对各类指令的占用消耗有一个基本概念,再细致一点的话还可以看看占用哪些硬件资源,p0156 代表可以再 0/1/5/6 几个硬件单元里任意一个执行,然后对着纸面代码进行一个大概评估。
后面有了 Intel IACA 以及 llvm-mca 后,自动化静态分析可以更加简单和准确。到这里,我们对仿射纹理映射做了一次性能静态分析,可以看得出定点数版本确实快,于是我们得到了一个性能更好的仿射纹理映射函数:

那么这样的静态分析准不准确呢?我们接着对两个函数进行动态性能评测:
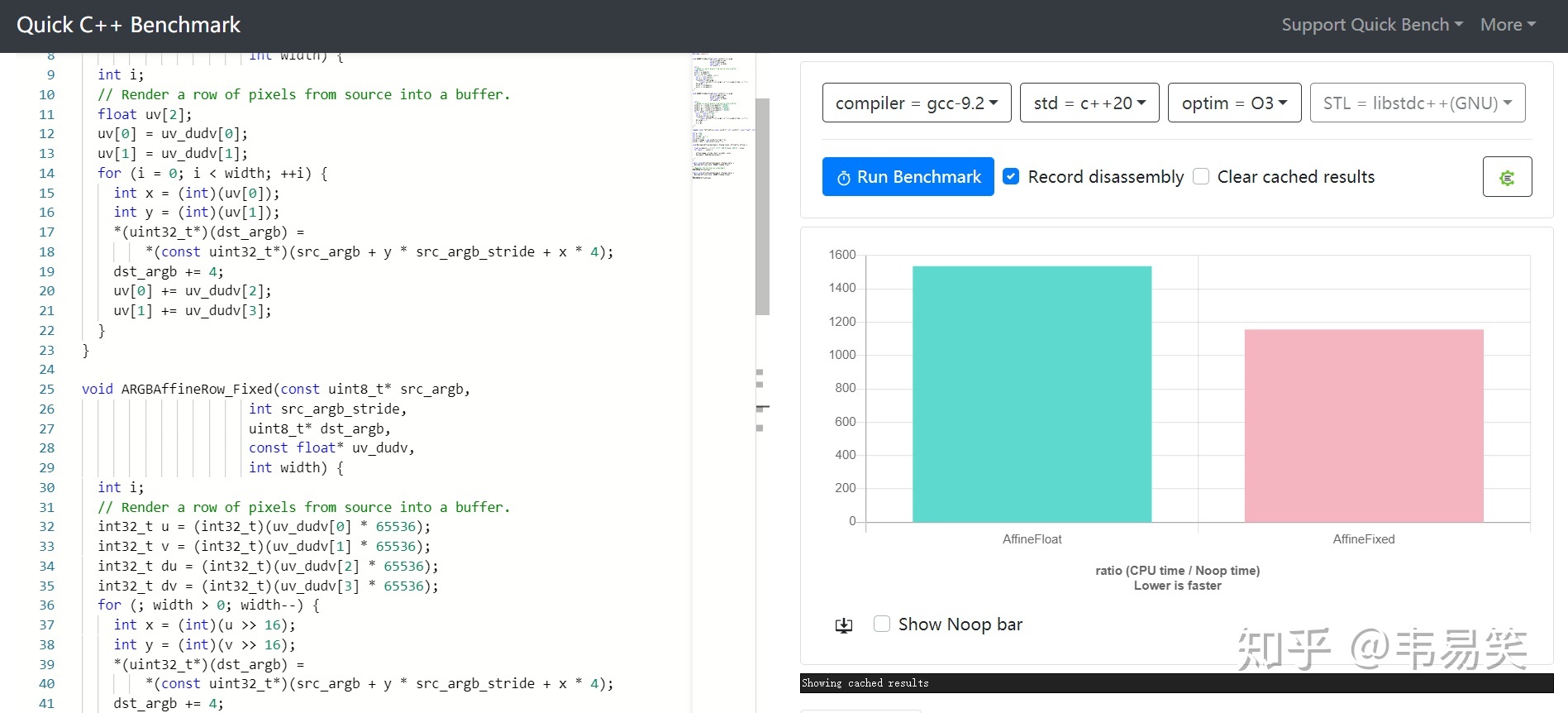
链接:http://quick-bench.com/FqOYuExcXoyHe_r6Bl1oSm0wUPE
在 gcc 9.2 下面,定点数比浮点数快了 30%,比我们之前静态分析的结论类似(4.58 比 3.37),但差距略稍许偏低没有纯周期计算出来的 35% 性能差距那么高,因为两边都平摊了 I/O 操作引入的延迟(这部分 mca 没法计算进去)。
那么我们继续切换编译器,换成 clang 9.0 :
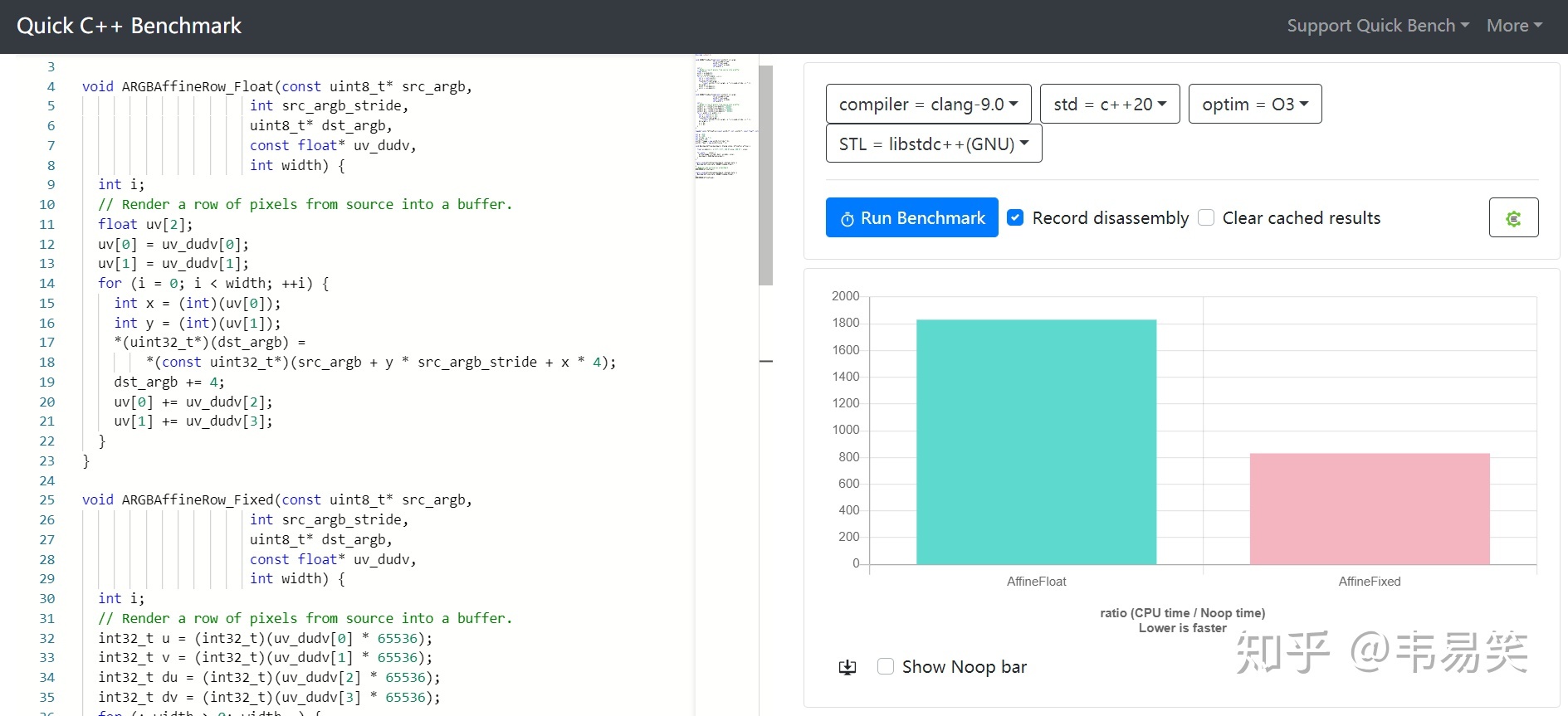
链接:http://quick-bench.com/RoUdH66MayHq6exmQ99mhODUN2w
可以看到性能提升了 2.2 倍,看代码生成,因为在 clang 下进行了矢量展开,定点数和浮点数都进行了循环展开,每轮循环一次性计算两个点,导致了更大的性能提升。
C 版本的定点数还可以继续用 SIMD 一次性算四个点的定点数坐标,性能应该还能提升一级。
定点数除了能在特定地方让你的代码性能提升数倍外,在很多对结果严格要求一致的地方,也会比浮点数更好,比如帧间同步的游戏,需要在 arm/x86 下面不同客户端保证同样的计算结果,这样浮点数就挂了,不同手机运算结果不同,只能用定点数来处理。
(PS:对于一些复杂运算比如 sin/cos 之类的三角函数,定点数一般用查表+插值进行)
最后,定点数是一个值得收藏到你编程百宝箱里的好工具,必要的时候能够帮到你。
![]()
