快除 255：到底能有多快？

真金不怕火炼，我先前在《C 语言有什么奇技淫巧？》中给出的整数快速除以 255 的公式：

#define div_255_fast(x)    (((x) + (((x) + 257) >> 8)) >> 8)

有人觉得并没有快多少，还给出了测试：

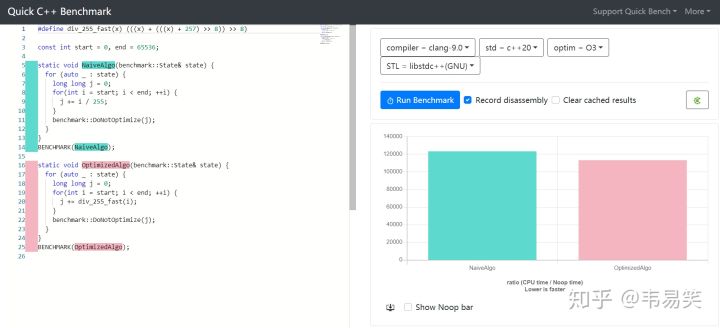
红色为 255 快除法的消耗时间，看他的测试好像也只快了那么一点，是这样的么？

并非如此，我们只要把测试用例中的 long long j 改成 int j 就有比较大的性能提升了：

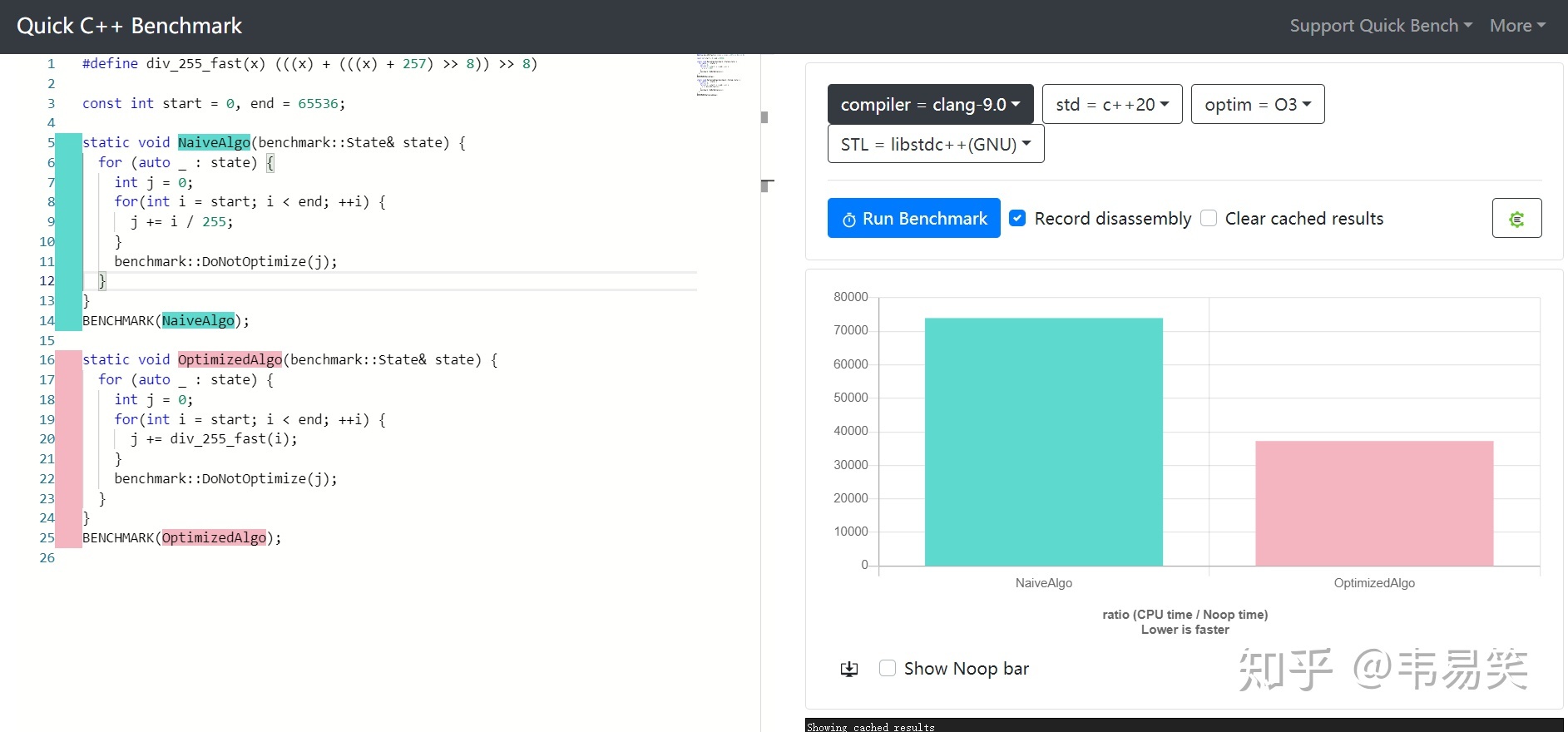
链接：http://quick-bench.com/t3Y2-b4isYIwnKwMaPQi3n9dmtQ

这才是真实的快除法性能。

原评测的作者其他地方都是用 int ，这里故意改成 64 位去和原始的 / 255 对齐，引入一个干扰项，得到一个比较慢的结果，到底是为了黑而黑呢？还是别的什么原因？

编译器生成的 / 255 方法是把 x / 255 换成定点数的 x * (1/255)：

（点击 Read more 展开）

static inline uint32_t fast_div_255_any (uint32_t n) {
    uint64_t M = (((uint64_t)1) << 32) / 255;   // 用 32.32 的定点数表示 1/255
    return (M * n) >> 32;   // 定点数乘法：n * (1/255)
}

这样定点数算法有一定误差，需要提高精度到 24.40 ，并且做四舍五入进位：

static inline uint32_t fast_div_255_accurate (uint32_t n) {
    uint64_t M = (((uint64_t)1) << 40) / 255 + 1;   // 用 24.40 的定点数表示 1/255
    return (M * n) >> 40;   // 定点数乘法：n * (1/255)
}

基本上这就是编译器所有优化打开，实际生成的 / 255 的代码，在 32 位整数范围内误差为零，可以发现 div_255_fast 比起定点数常算法，快就快在无需要乘法，同时可以用 16 位整数就完成所有运算，不需要 64 位整数运算，适合 SIMD 寄存器里同时用多个数据并行求值。

32 位系统算 64 位定点数效率比 64 位系统还要低，性能差距还会更加明显。

—

PS：知乎上 @朱元 把 256 提取出来，又优化了一个版本：

#define div_255_fast_v2(x) (((x) + 1 + (((x) + 1) >> 8)) >> 8)

性能再次提高：

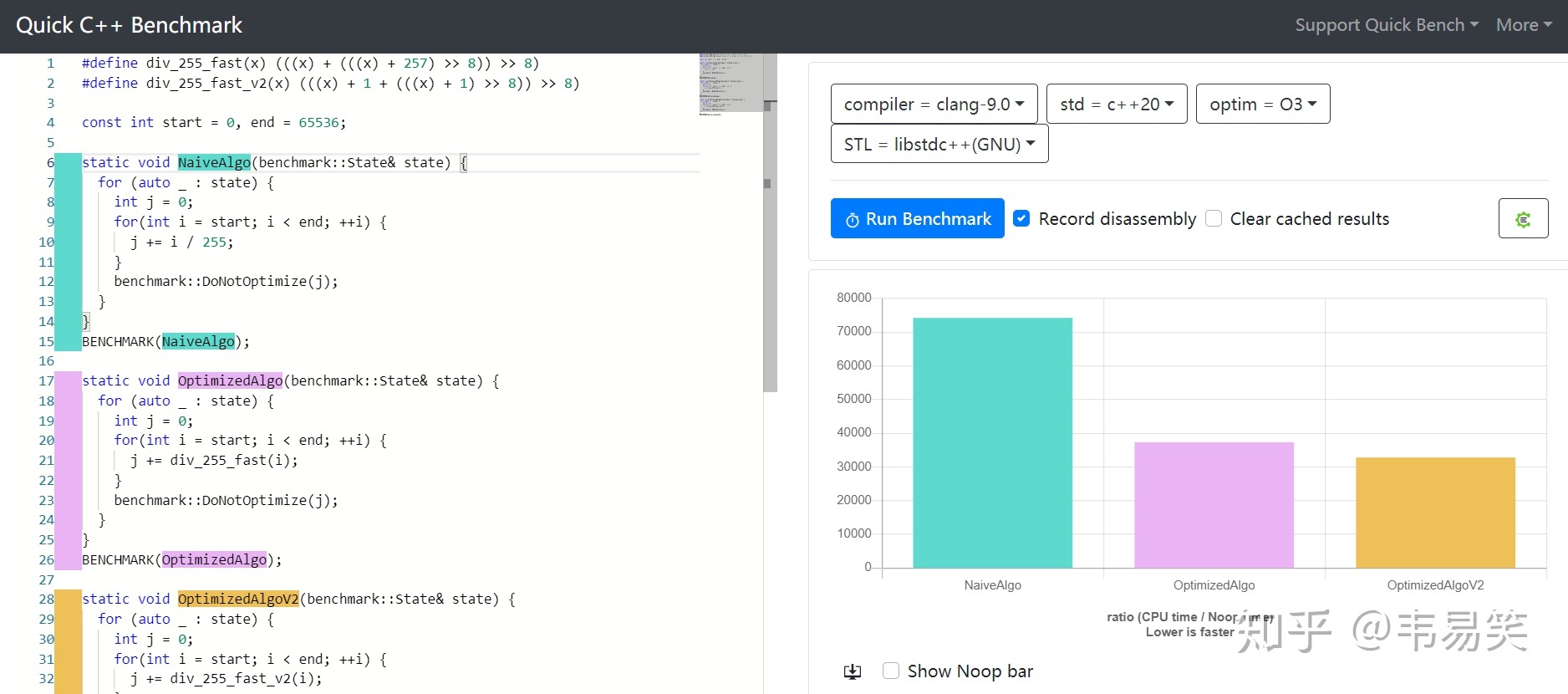
链接：http://quick-bench.com/srEkdpQlplhERyLN3YZkqCVhLH8

注意最右边黄色部分：div_255_fast_v2 。